Brian Greene: The Elegant Universe
with Related Information from Other Sources
Summary by Michael McGoodwin, prepared 2000
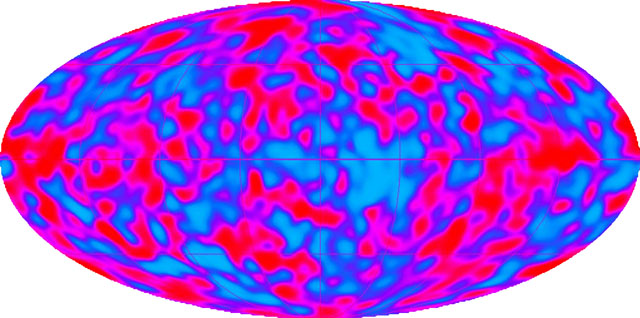
Cosmic microwave background radiation fluctuation after subtraction of dipole and
galactic emission
(This image is
modified from a COBE satellite image at http://aether.lbl.gov/www/projects/cobe/COBE_Home/DMR_Images.html.)
For more current images, see the WMAP project.
Notes: In 2000, I prepared this summary rather hastily and for my own benefit to improve
at least my
retention (if not my understanding) of the concepts discussed in the book and have added related subject matter gathered from
various books and some web sites I came across. I offer this summary to assist others
also interested in reading this interesting and challenging book. I have not attempted to
present a comprehensive summary. Greek letters and other symbols that are not
available with standard HTML are represented spelled out in curly braces, e.g. {tau}.
The usage "1E44" means 1 X 1044 . I would be pleased to
be notified of any errors.
Chapter 1
Tied Up With String
The pillars of 20C physics, quantum mechanics and general relativity are mutually incompatible
particularly at the subatomic level at which quantum effects are most apparent. BG recalls earlier conflicts in theories pertaining (1) to the speed of light for moving observers, resolved by Einstein's special theory of relativity, and (2) the problem of the apparent instantaneity of gravitational effects resolved by general relativity's warp of space.
Protons are not fundamental but composed of quarks
(confirmed at SLAC 1968), named by Murray Gell-Mann after Finnegan's Wake: protons have 2 up-quarks and a
down-quark, and neutrons 2 down-quarks and an up-quark. Reines and Cowan 1950 found evidence for
neutrinos (now termed electron-neutrinos), and the muon was found in the 1930s. Charm and strange
quarks also found, along with muon neutrino and tau neutrino. All of these particles have antiparticles. The family of matter are now grouped in 3 families (p. 9) with analogous particles (e.g., electron, muon, and tau occupying similar positions in each family). All matter found to date is in one of these 3 families and their antimatter counterparts.
The fundamental forces and their force charges are
the strong force (they glue quarks together, possible charges are red, green,
and blue), electromagnetic (e.g., the electric charge of quarks can be 2/3 or
-1/3 ), weak force (related to beta decay, charge can be 1/2 or -1/2), and gravity.
These forces are mediated by the gluon, the photon, the weak
gauge bosons W and Z, and the graviton resp. (with relative strengths of 1E44, 1E42, 1E39, and
1, resp.)
String theory posits that quarks are not point-particles but contain a loop of vibrating energy that resolves the conflict between
General Relativity and Quantum Mechanics (QM). The various resonant vibrational modes account for the different forms matter takes in terms of mass and force charge (e.g.,
electrical charge, weak charge, strong charge). String theory has been suggested as a candidate for the "Theory of
Everything (TOE)" on which we might build our understanding of the world
[i.e., it would unite the gravitational force with the electric, weak, and
strong forces]. However, the computations may be impossibly difficult
and thus cannot justify a completely reductionist view. String theory is in its early stages, "a part of 21C physics that fell by chance into the 20C"
(Edward Witten). No one knows the exact equations. It is part of a grander synthesis called M-theory.
Chapter 2
Space, Time, and the Eye of the Beholder
Reviews the Maxwell equations mid 1800s uniting the electrical and magnetic forces. He found that light travels at a fixed speed. Einstein 1905 studied the speed of light as observed by observers
[here arbitrarily labeled by me M and S] moving relative to each other and found that each would measure it to be the same. However, the uniformly moving observer M experiences time slower relative to a "stationary" observer S ("time dilation") and also S measures M's lengths to be shorter
("Lorentz
contraction"). But concept of motion is relative and each observer will make these observations about the other, with there being no absolute frame of reference for force-free motion. Einstein concluded that the laws of physics for the 2 observers must be the same ("invariant") and that therefore they must experience the same light ray as having the same speed in vacuum (670 million mph)—a symmetry.
Discusses consequences of light speed being constant, including the downfall of Newtonian
mechanics (developed by Isaac
Newton 1643 - 1727). Things that are simultaneous to M are not necessarily so to
S, due to finite time for light to travel. A universal clock does not exist. Time is what is measured by clocks, something undergoing regular cycles of motion. Posits the "light clock" though experiment, 2 mirrors with a photon
traveling back and forth held by M. The photon will be seen by S to travel further and therefore S's measure of M's time must be slowed down for the photon to travel at a uniform speed to S. The rate of ticking becomes slower and slower as the relative speed increases. This is an intrinsic property of time and not dependent on the means used to measure it.
Tm = Ts/sqrt(1-v2/c2). In real life, high speed muons appear to disintegrate slower that those at low speed, though they experience the same amount of life. Each observer experiences that the other's clock is running slower (and this holds even if one takes into account that a transmitted timing signal is delayed by the finite speed of the
photons).
Minkowski and Einstein viewed motion as occurring
therefore in both space and time, or 4D spacetime. Einstein declared all objects travel through spacetime at the speed of light. [spacetime
position x = (ct,
x1, x2, x3); velocity = dx/d{tua} which has magnitude c, here
{tau} is the "proper time" defined by d{tau}2 = dt2 - c-2(dx12+dx22+dx32]. He also concluded the equivalence of matter and energy through
E=mc2.
Chapter 3
Of Warps and Ripple
The invariance of the speed of light posited by special relativity was incompatible with Newton's universal theory of gravity F =
G*m1*m2/r2 because it assumes an infinite speed of transmitted force changes when the mass of an object changes. Even Newton suggested gravity must be caused by an agent and not by a force acting at a distance. Einstein resolved this with general relativity, after realizing the equivalence principle, the close interconnectedness of the experience of gravity to uniformly accelerated motion. He viewed matter as curving or warping spacetime as if on a saddle-like surface, so that for example a spinning circle [drawn on a such a surface] has a longer circumference than if there were no curvature. Both time and space are warped and gravity is this warpage. The analogy of a bowling ball depressing a plane surface is given. The warpage is transmitted by gravity waves which move at the speed of light. Objects move through spacetime according to the shortest or easiest possible path
[geodesic], and these paths will be curved near masses. In John Wheeler's words, "Mass grips space by telling it
how to curve, and space grips mass by telling it how to move." An observer near a large mass would find his clock ticking much slower, and there is no symmetry
with respect to an observer who is not near the mass—there is no equally valid
perspective when acceleration is present.
General relativity was thought to have been verified by the famous prediction of the bending by 1.75
arc seconds of starlight passing by the sun during a solar eclipse, confirmed by Eddington 1919 (an experiment whose reproducibility was subsequently questioned).
Karl Schwarzschild predicted the existence of black holes 1916 (named such by Wheeler), in which matter inside the event horizon would fall in and nothing would escape, not even
light. At the center of the Milky Way is prob. a c. 2.5E6 solar mass black hole, and
black holes up to billions of solar masses may exist. Einstein was disturbed when he calculated that the universe must be expanding and fudged his calculation with a "cosmological constant".
But Hubble confirmed the expansion. Backward extrapolation predicts
15 billion years ago an infinitely squeezed state of the universe, at which time the "Big Bang" occurred. The calculations of
general relativity are quite accurate but cannot cope with the compressed state preceding the Big Bang, and is incompatible with quantum mechanics.
Chapter 4
Microscopic Weirdness
Reviews quantum mechanical phenomena at the microscopic level. By 1928, most of its equations were in place, but it is difficult to understand why it works!
Reviews the problem of the spectrum of the black body radiation, which by classical computation should have infinite energy, since an infinite number of possible resonant
electromagnetic (EM) waves must each carry the same energy. By Planck's hypothesis 1900 that EM wave energy occurs in quantized increments
(h*f where f= frequency Hz and h = Planck constant), the total energy combining the various vibrational modes is finite because above a certain threshold of energy, there can be no contribution. The predicted spectrum is in accord with experiment. Here the Planck constant h = 662 E-36 Joule sec or 6.624 x
1E-27 erg sec. Einstein deduced that
the photoelectric effect found by Heinrich Hertz 1885 was due to light
occurring as individual particle-like packets or quanta of energy (later termed photons by Gilbert Lewis), and that the color of the light and not its intensity
primarily determined whether the PE
occurred at all [and the ejection velocity of the photoelectrons: beam intensity
only affects the number of electrons ejected, but does not change the ejection
velocity; beam color is determined by its photon energy h*f or h*{nu} or h-bar * {omega} where {omega} equals angular frequency in radian/sec and h-bar = h/2{pi} = 1.06 E-34 kg m^2
sec^-1]. Thus light seemed to have both particle and wave properties. Young's double-slit experiment in early 1800s had shown light to have wave properties by exhibiting interference
pattern etc. This pattern was later found to persist even if the photons pass through one at a time. Thus a wave-particle duality for light existed.
Louis de Broglie 1923
proposed
this duality for all matter, shown for the electron by Davisson and Germer 1920s.
[Schiff Quantum Mechanics 2nd Ed: In scalar form, wavelength {lambda} = h/momentum. Also momentum = h-bar*k where k is the wave vector, and rest energy E =
mc2 = h-bar*{mu} where {mu} is the rest frequency of a particle.]
The Schrödinger wave equation
[1925-6] was refined
and interpreted by Max Born 1926, who proposed that an electron and matter in general must be viewed from the standpoint of probability.
[I.e., the position probability density, which equals the square of the absolute value
(magnitude or amplitude) of the complex {Psi} function, is such that
P(r,t)dxdydz gives the probability of finding a particle in this
infinitesimal voxel, and the integral over all space of P(r,t) equals 1]. Exact outcomes of experiments
thus cannot be predicted in QM. Einstein objected to this vagueness and
randomness but was proved wrong. There is still debate as to what this all
means however. Feynmann emphasized how attempts to localize an electron perturbs it and changes the outcome. He suggested electrons pass through all slits
in an experiment and traverse every trajectory, but that the sum-over-paths is the resultant probability distribution, wherein for large objects all paths but one cancel each other
out [this method is an alternative to calculating the probability wave
function].
Werner Heisenberg's uncertainty [or
indeterminacy] principle 1927 showed that certain conjugate physical quantities [Schiff: "canonically conjugate in the Hamiltonian sense"]
could not be
simultaneously known precisely: e.g., the order of magnitude of the product of the uncertainties of position {delta}x and momentum
{delta}px >= h-bar [some
authors state one-half h-bar]. Other canonically conjugate pairs are angular position/angular momentum, and time/energy. Bohr termed
these quantities complementary and this effect the complementarity principle, concluding that atomic phenomena cannot be described with the same accuracy as in the macroscopic world inasmuch as more precise measurements for any experiment cannot be made than the limits set by the uncertainty
principle (for example, the measuring photon perturbs the position or momentum
of the particle). A photon can only pinpoint
the location of an object to within one photon wavelength. If an electron is confined to a space of decreasing size, its motion
(momentum) increases wildly due to "quantum claustrophobia" since
{delta}p*{delta}x>= h-bar and as {delta}x decreases, the momentum must increase.
There is also quantum tunneling, in which a particle classically lacking the requisite energy to overcome a barrier is able to borrow
the energy to do so [or at least to tunnel through the barrier if it is narrow enough].
Chapter 5
The Need for a New Theory;
General Relativity vs. Quantum Mechanics
Under extreme conditions of great mass or very
small scale, the success of General Relativity breaks down and nonsensical
predictions occur—for instance, at the time of the Big Bang or at the center of
black holes. In these situations, we need a quantum mechanical version of
general relativity.
The uncertainty of the Heisenberg principle is
intrinsic to nature and not a result merely of attempting to make
measurements—e.g., the quantum claustrophobia occurs even in the absence of a
measurement. Even in so-called empty space, the uncertainty principle
tells us that there is tremendous activity: energy fluctuations cause an
electron and antielectron to erupt into existence and to subsequently annihilate
one another. "Macroscopic averaging obscures a wealth of microscopic
activity." The mathematical technique developed by Dirac, Pauli, etc.
to deal with this disorder is called quantum field theory. The Schrödinger wave equation
was found to be only approximate and unsuitable for very small microscopic
domains because it ignored special relativity.
The body of theory incorporating special relativity is
called quantum electrodynamics (QED), an example of a relativistic quantum field
theory or a quantum field theory QFT. QED has been extremely successful in predicting
natural phenomena. E.g., Hinoshita has made electron predictions
accurate to better than one part in one billion. Quantum electroweak
theory was developed to unite the weak and the electromagnetic forces (Glashow,
Salam, and Weinberg) in a common form at high temperatures and energies; at
lower energies the individual forces "crystallize out" (analogous to a
phase diagram) in a symmetry-breaking process. Quantum chromodynamics
(QCD) was
developed to quantify strong force interactions—it presents extremely complex
computations. [A theory unifying the strong force with electromagnetic and
weak forces is called a Grand Unified Theory or GUT]... This combined body of highly
successful theories is termed the Standard Model (SM)and has been very successful in
making predictions. However, the Standard Model does not explicitly
include quantum gravity or the graviton.
In the Standard Model, messenger particles carry
the forces (i.e., gluon, photon, weak gauge bosons W & Z [and the graviton]).
An electromagnetic field is conceived as a swarm of photons which shoot back and
forth between the two objects that are interacting. When protons repel
each other, it is as if the messenger carries the message as to how they should
interact.
Discussion of the importance of symmetry in
physics. E.g., the symmetry of quarks means that the interaction of 2 red
quarks is the same if 2 green quarks are substituted for the red. The
universe thus exhibits strong force symmetry in that the strong force is not affected by
force-charge shifts. The strong force is an example of a gauge symmetry...
Because of quantum fluctuations, QM predicts
empty space must have undulating gravitational field, an effect that becomes
more and more apparent as the scale decreases. At tiny scales, there is
violent warping and turbulence, so called quantum foam (Wheeler). Thus at
very small scales, the smooth spatial geometry required of general relativity is
destroyed. Calculations attempting to merge general relativity and
gravitation with quantum mechanics thus fail due to resultant infinities
(singularities).
The fabric of space appears smooth except at the ultramicroscopic level.
The scale on which this problem emerges is the Planck
length = sqrt(h-bar*G/c3) = 1.616x10-33 cm (some
authors use h and obtain 4x10-33 cm). This is an important
(though controversial) incompatibility, despite the fact that it only occurs at
this tiny scale, and the resolution of this lies in superstring
theory.
Chapter 6
Nothing but Music
The Essentials of Superstring Theory
String theory invites a musical metaphor of
vibrating strings (in the standard model, fundamental particles are
point-like). The strings are on the order of the Planck length in
size. All matter and forces are proposed to arise from strings. The
theory began with Veneziano 1968, who found that certain properties of the
strong nuclear force followed the Euler beta-function and in 1970 Nambu et al.
suggested this meant that they could be represented as vibrating strings.
Certain predictions of this model were successful, but it was overwhelmed by the
success of the standard model. String theory postulated additional messenger-like particles, and in 1974 Schwarz and Scherk realized that they
matched with the expected properties of the graviton. They suggested the
theory included quantum gravity but was not confined to this. But there
were unresolved conflicts between string theory and QM until 1984, when Green
and Schwarz found a way to resolve these, and that the resultant theory could
incorporate all 4 forces and all of matter as well. The "first
superstring revolution" resulted, in 1984 - 1986. "Numerous
features of the standard model ... emerged naturally and simply from the
grand structure of string theory." But so far even the equations have
not been precisely determined, much less solved. Edward Witten 1995 began
the "second superstring revolution" by introducing certain ways of
partially dealing with the complexity.
Strings are either truly fundamental and
indivisible or composed of smaller constituents—this is an unanswered question,
but the author for discussion purposes "will take strings to be nature's
most fundamental ingredient". Numeric predictions are possible from
string theory that must simply be presumed in standard model to be measured
input. The standard model is too flexible and cannot be used to explain
the properties of fundamental elementary particles. In string theory,
these properties (such as mass and force charges) emerge as resonances, specific
vibrational patterns [note 7 p. 398 provides a hint of some of the details]. Discusses vibrational modes for open and closed
strings. Greater energy means greater mass (gravitational charge) and
indicates a higher vibrational mode. Similarly, electric charge, weak
charge, and strong charge are carried by a particular string vibration
mode. One mode matches the graviton exactly. Each elementary
particle consists of a single string (all of which are fundamentally identical) undergoing
a characteristic resonant vibration ("different
notes"). Thus the promise of a Theory of Everything, in which
fundamental properties could theoretically predicted—but such euphoria is
premature and these predictions have not yet been made because of the
computational complexity.
String tension varies but is very high at around
1x1039 tons (the Planck tension)—transmitted force is inversely
proportional to the string tension. This causes them to contract to
very small size (c. Planck length). The vibrational energy is
high and occurs as whole number multiples of a minimal energy denomination, the
Planck energy corresponding to a Planck mass of
1E19 times the rest mass of the
proton (thus Planck mass is ~ 5.5E-8 kg). Quantum jitters is a form of negative energy that cancel out all
of this huge mass except the relatively low net energy. In particular, the
graviton candidate has a perfect jitter cancellation resulting in a zero mass
particle (as expected by its capability of traveling at the speed of
light). Actually proving through computations that these cancellations
occur is not currently feasible. Of the infinite potentially possible
vibratory string modes, only a few are light enough to be identifiable at
typical current experimental energy levels obtained in accelerators
(correspondingly, the Planck
mass cannot be attained experimentally currently, and heavy particles in any event are probably
unstable).
"String theory softens the violent quantum
undulations by "smearing" out the short distance properties of
space." When taking measurements in a system, the size of the probe
particle determines the potential maximal resolution, i.e., smaller probes can
determine finer detail. For small probes such as photons, its
"size" is its quantum wavelength. But the string's inherent
spatial extent prevents is from probing the structure of anything substantially
smaller than its own size. Moreover, Gross and Mende 1988 showed that
increasing the energy of a string does not increase its ability to probe smaller
sizes, since in fact they grow in size. This smearing is due to quantum
jitter and to its own inherent spatial extent. "There is a limit to
how finely we can probe the universe." In the point-particle
paradigm, particle interactions occur at a precise location and time regardless
of the state of motion of two observers. But interactions of strings,
which can be represented as a "world sheet" are more spread out, and
separate observers in different states of motion may observe the time of first
contact to be different (p. 162). This "spreads out the force's
punch" and "dilutes its ultramicroscopic properties" so that
"calculations yield well-behaved finite answers." I.e., the
smearing smoothes out the ultramicroscopic jitters of space at sub-Planck length
distances—the smearing cannot be removed. The incompatibility of gen. relativity. and QM is resolved.
String theory predicts the exact properties of
the graviton and gravity is an intrinsic component of string theory. With
the 2nd string revolution of 1995, strings are now conceived as having more than
1 or 2 dimensions
Chapter 7
The "Super" in Superstrings
This chapter discusses the role of
aesthetics in discovery in physics, and in particular the search for and
desirability of symmetries. Physicists assume the laws of nature are fixed
[at least in our local universe within a multiverse], that every location in space and time exhibits
the same laws. Special relativity says the laws are the same for observers
in uniform force-free motion with respect to each other. The equivalence
principle of general relativity extended the symmetry of special relativity to
make the laws of physics identical for
observers moving and accelerating with respect to each other (motion
symmetry). The laws of physics should also not care about the angle from which
observations are made, so rotations should not change them (rotational
symmetry).
The spin intrinsic angular momentum of electrons was
proposed by Uhlenbeck and Goudsmit 1925, who used this to explain spectral
line-splitting in the presence of a magnetic field. This spin was
inherently quantum mechanical and intrinsic to the electron, and occurred at
only one rate, up or down. All fundamental matter particles (i.e., fermions such as quarks plus
the leptons such as electron, muon, and tau) have half-integral spin (i.e., with
magnitude h-bar*1/2 or "1/2"). The force carriers are bosons
with integral spin=1 (except
the graviton, which is postulated to have spin 2). In string theory, the spin is associated with
the pattern of vibration: the graviton was predicted by Scherk and Schwarz to
have spin-2 and no mass.
When spin is considered, an additional symmetry
("supersymmetry") becomes mathematically possible. Supersymmetry
is not
associated with any easily expressible quantity [The author does not attempt
to define it.] In the 1970s,
supersymmetry was found to predict the existence of superpartners for each known
particle, with spins predicted to differ by 1/2 (none of these have yet been
demonstrated). [One website states "every fundamental matter particle should have a massive "shadow" force carrier particle, and every force carrier should have a massive "shadow" matter particle. This relationship between matter particles and force carriers is called supersymmetry."
The superpartners of fundamental fermions have been tentatively named by adding s-: thus, the
squark, selectron, and sneutrino (these superpartners all have spin 1). The
superpartners of the force particles are named by adding -ino: photino, gluino, wino, and zino
(these superpartners will have spin 1/2)
Even without string theory, there are compelling
reasons to suggest the existence of supersymmetry. (1) It is
aesthetic. (2) The standard model requires extremely finely tuned particle
parameters, whereas in supersymmetry there is a canceling out by bosons and
fermions occurring in pairs that removes this extreme sensitivity. (3) It
can lead to a grand unification of strong and other forces with gravity...
Georgi, Quinn, and Weinberg computed that the strengths of the 3
nongravitational forces become approximately equal at the scale of 10,000 times the Planck
length, exactly equal if supersymmetry is incorporated.
But supersymmetry is especially appealing in
string theory, and makes it "superstring" theory--contributors have
been Ramond, Gliozzi, Scherk, Olive... Superstring theory avoids problems
with tachyons (particles traveling faster than light)... However, there is an embarrassment of riches, inasmuch as
there are 5 seemingly separate supersymmetric string theory candidates: Type I theory,
Type IIA, Type IIB, the Heterotic Type O(32) theory, and the Heterotic type
E8 X E8 theory. Witten has shown that these types
are all parts of a larger synthesis.
Chapter 8
More Dimensions Than Meet the Eye
In 1919, the Polish mathematician Theodor
Kaluza proposed the existence of additional spatial dimensions. In the
same way that an ant walking on a garden hose seen at great distance appears to be on a
one-dimensional (line) surface, the extra dimensions can be conceived as being tightly
rolled up so they do not appear obvious to the macroscopic observer...
This concept was made more explicit by Oskar Klein 1926... The extra
dimension might have the form of circles or other forms having sizes as small as
the Planck length. The idea of extra tiny dimensions is called
Kaluza-Klein theory.
Analogy to Flatland organisms on a garden
hose. Kaluza analyzed general relativity with one extra dimension and
produced the Maxwell equations, uniting general relativity with Maxwell's theory
of light. His ideas were ahead of his time and were abandoned until
revived in the 1970s. The extra dimensions were assumed to be smaller than
those which we can currently probe. The most promising formulations
incorporate supersymmetry. Strings inhabiting a universe with higher
dimensions have more independent vibrational directions [?modes]. When 9
spatial dimensions were assumed, problematic negative probabilities dropped out,
so nine spatial and one time dimension rendered 10 spacetime dimensions.
In the 1990s, Witten showed that 10 was an approximation and that the actual
value should be 11 spacetime dimensions. (There is nothing to prevent
additional time dimensions.)
The extra dimensions probably take the form of
6-dimensional geometrical shapes called a Calabi-Yau space or shape, of which
there are many thousands of members.
Chapter 9
The Smoking Gun: Experimental Signatures
Greene cites difficulty in obtaining any
experimental verification, and the opposition that has been expressed to such an
unprovable theory (e.g., Glashow), along the same lines that theology undermined
medieval science... It is not possible to do research at the Planck length
level. The necessary accelerator would need to be the size of the
universe... It will be necessary to search for indirect confirmations of
the theory. E.g., Candelas, Horowitz, Strominger, and Witten suggested
that there is a family of particles corresponding with each additional hole in
the Calabi-Yau space. Perturbation theory has been the traditional way to
make difficult calculations involving multiple variables, especially when one
effect (like the sun in computing planetary orbits) dominates...
The existence of the superparticles predicted by
superstring theory will be sought with the CERN Large Hadron Collider under
construction in Geneva for operation in 2010. Also, fractionally charged
particles have been predicted and will be sought, though likely to have very
large mass ~Planck mass. Even less likely possibly related phenomena to be
found are macroscopic strings, nonzero neutrino mass, disintegration of the
proton, decays of quarks, new forces, dark matter, a revised cosmological
constant, etc. Whole generations of physicists will labor with superstring
theory without the benefit of constant experimental results to correct erroneous
conclusions.
Chapter 10
Quantum Geometry
Reviews Georg
Riemann's view of curved spaces,
which is the mathematical core of general relativity. Quantum geometry is
the mathematical core of string theory, though it is not as ready-made as
was Riemann's geometry for Einstein. Riemann drew on Gauss, Lobachevsky,
Bolyai etc. and evaluated the measure of distances in curved space.
Einstein concluded the curvature of space is gravity.
The Big Bang occurred 15 billion years ago.
If the critical density of the universe (1E-29 gram per cc) is exceeded, the
expanding universe will halt and reverse and collapse. String theory is
needed to evaluate the extremely compressed early state, and sets a lower limit to the ultimate
size of the Big Crunch (the Planck length). This limit arises from string
wrapped configurations called winding modes, in which there is a minimum length
and mass... Strings that attempt to collapse smaller than the Planck
length begin to expand as follows. For every large circular radius, there
is a corresponding small circular radius for which the winding energies of the
corresponding strings are equal, and there is no physical distinction between
these geometrically distinct forms... Thus when one tries to make a
measurement using the lightest (easiest) of the string modes, the measured
result will always be larger than the Planck length. When shrinkage to
below the Planck length is attempted, the crunch becomes a bounce.
Ultrashort distances and their infinities are thereby avoided—sub-Planck-scale
distances are simply inaccessible and meaningless... Brandenberger, Vafa,
etc. used these results to suggest a new cosmology where the big crunch is
Planck length in size. Regardless of the shape of the compact dimensions,
there is probably a limiting size.
Greene discusses his, Plesser, and Candela's
discovery of a key string property, mirror symmetry. Mirror manifolds are
physically equivalent yet geometrically distinct Calabi-Yau spaces which exist
for certain Calabi-Yau spaces that were previously thought to be unrelated but
are connected through string theory. This pairing allows what would be a
very difficult calculation of a particular Calabi-Yau space to be made on the
simpler mirror symmetric Calabi-Yau space. One example is the counting of
spheres that can be packed inside the Calabi-Yau space...
Chapter 11
Tearing the Fabric of Space
Greene discusses concept of wormhole, "a
bridge or tunnel that provides a shortcut from one region of the universe to
another". Can space tear? In 1987, Yau and Tian showed that
certain Calabi-Yau shapes could be transformed by puncturing their surfaces and
sewing them back up according to a pattern... They envisioned an internal
sphere which is pinched and torn leading to a flop-transition as if the sphere
is flopped into a new orientation... By adding the mirror perspective,
Greene showed that a space-tearing flop transition for one Calabi-Yau space was
perfectly well behaved in the mirror, excluding the possibility of a catastrophe
in the original...
Homage to Edward Witten's brilliance.
Greene describes his successful effort to verify using a computer program that space tearing
transitions (topology-changing transitions) are part of string theory.
Witten added that strings encircle the tear, shielding the universe from
catastrophe... Papers published 1993...
Chapter 12
Beyond Strings: In Search of M-Theory
Greene summarizes the problems with string theory
apparent by the 1980s. There were too many candidates. The exact
form of the equations was not known. In 1995, the second superstring
revolution began by Witten's suggestion that the 5 candidates are all related
and part of an overall synthesis or framework called M-theory. M-theory
requires 10 space dimensions, 11 overall dimensions including time.
Previously, one space dimension had been "overlooked" because the
calculations made were only approximate. M-theory not only includes
vibrating one-dimensional strings ("one-branes") but more extended
objects such as 2-dimensional membranes ("two-branes"), 3-D blobs
("three-branes"), and other even more complex objects. Moreover,
the techniques commonly employed to facilitate approximate calculations,
perturbation theory (originally applied to astronomical orbits), failed in some
cases of string theory. Perturbation theory helped in dealing with virtual
string pairs that transiently materialize, even in multiple numbers, but are the
computations correct? The answer depends on the value of the "string
coupling constant": if less than one (weak coupling), the perturbative
approach is likely to be valid, but if the coupling constant is one or greater
(strong coupling), the likelihood or higher order virtual pairs affecting the
calculations is greater and perturbative theory cannot be used. The value
of this constant is currently not known, and approximate string equations have
proven too flexible to be useful in aiding this determination.
Witten introduced the concept of duality at the 1995
string conference at USC. This concept allows the use of perturbative
theory for a wider range of problems. Examples of duality are (1) the
string pairs resulting from mirror symmetry and (2) the equivalence of string
computations at circular dimensions of R and 1/R. Witten suggested the
five competing theories are actually dual (each has an equivalent string in at
least one other theory), and that a string exhibiting strongly coupled behavior
in one theory has a dual description with weak coupling under another theory,
thereby allowing calculations to be made with perturbative theory. He also
included a 6th theory to complete the dualities: 11-D supergravity.
Through the use of supersymmetry and this dualism, previously intractable
properties can theoretically be reduced to fewer possibilities and can be
calculated indirectly... A set of states proposed by Bogomol'nyi, Prasad,
and Sommerfield ("BPS states") specify a minimum mass condition which
is conducive to calculation without use of perturbative approach, i.e. the
masses and charges calculated are nonperturbative yet involving strong coupling
and provide useful known results.
"These strong coupling characteristics of
Type I string theory exactly agree with known properties of Heterotic-O string
theory when the latter has a small value for its string coupling
constant." This "suggests that the physics of the Type I theory
for large values of its coupling constant is identical to the physics of the
Heterotic-O theory for small values of its coupling constant." This
is a strong-weak duality. Proof of this will be difficult to achieve, but
theorist believe duality is likely to be correct as well as helpful in making
calculations. Type IIB strings are self-dual. Moreover, Type IIA
strings in a universe of radius R have identical physics to Type IIB strings in
a universe of radius 1/R.
Supergravity theory preceded string theory:
"supersymmetric quantum field theories that try to incorporate general
relativity", but these met with failure, though the most nearly successful
were those incorporating 10 (or 11) dimensions. Witten 1995 argued that
when its coupling constant is increased, the 10-dimensional Type IIA string
theory approximates 11-dimensional supergravity, the added dimension
becoming more and more apparent as the coupling constant rises... Witten and
Horava suggested also that as Heterotic-E theory becomes more and more strongly
coupled (i.e., the coupling constant increases), an 11-th dimension becomes
increasingly apparent as the strings get stretched into cylindrical
membranes. This added dimension is not one in which the vibration can
occur. A similar description applies to Type IIA strings, though these
stretch into a 2D toroid surface.
For low energies, the postulated but as yet
undefined 11-D theory is the former supergravity quantum field theory.
Witten has named the overarching theory M-theory (for Mystery, Mother, Membrane,
Matrix, etc.). All 5 string theories are joined together by
dualities as is 11-D supergravity—we can pass between any one theory to any
other via the central M-theory (as with a hub and spoke analogy) by means of
varying the coupling constant and various geometric parameters. In each of
the 5 string theories, the strings can actually be 2-dimensional
membranes. In fact, they can theoretically have up to 9 dimensions
(nine-branes, generically "p-branes"). However, all but the
1-dimensional strings will be very massive and are unlikely to play much of a
role in routine conditions and can probably be ignored. A key unanswered
question is what is the actual position in the synthesis of the 6 theories that
actually describes our universe.
Chapter 13
Black Holes: A String/M-Theory Perspective
Reviews contributions of Hawking, Penrose,
etc. Black holes are similar to elementary particles inasmuch as they have
no identifiable internal structure: they can be completely characterized by
their mass, force charge, and spin angular momentum. Discussion of problem
of collapse of space in the region of a black hole and possible
cataclysm—Andrew Strominger proved this will not happen due to wrapping of
three-branes about 3-D sphere, etc... Greene and others realized that a
collapsing 3D sphere can lead to a tear in a Calabi-Yau space with reinflation of the sphere now as a 2D sphere (a "conifold transition")...
"One Calabi-Yau shape could, in essence, transform itself into a completely
different Calabi-Yau shape." with a different number of holes (in fact, a
Calabi-Yau space can transform into any other Calabi-Yau space)...
Regarding black holes, the author suggests that string theory predicts they can
undergo this transition to a massless elementary particle, a photon, through
what is essentially a phase transition. Black holes and photons are simply
"two phases of the same underlying stringy material".
What happens to entropy when matter is consumed
by a black hole? Bekenstein with Wheeler 1970 addressed this question,
suggesting that they must have entropy to satisfy the 2nd law of thermodynamics,
and that the area of the event horizon would be a measure of the entropy of the
black hole. Hawking
1974 has shown that black holes have a temperature, and radiate black-body
radiation due to consumption of one but not the other of a pair of virtual
photons that come into existence just outside the event horizon. The
apparent temperature of a black hole implies there is entropy associated with
the black hole. [The predicted
temperature is (6 x 10-8/M) Kelvin, where M = number of solar
masses. Thus small black holes have higher temperature and more rapidly
radiate away their energy and even eventually evaporate.]
String theory (via Strominger and Vafa 1996
publication) answers the question: where is the disorder in the high entropy of
a large black hole?... Their calculation, made on idealized
"designer" black holes, agreed with the Hawking/Bekenstein prediction,
an important verification of string theory.
The determinism of Pierre-Simon Laplace
was replaced by a lesser quantum determinism, in which future probabilities are
determined via wave functions but actual outcomes are not precisely
predictable. Hawking showed that anything sucked into a black hole has its
wave function sucked in as well, so information is apparently lost forever
(unappealing to physicists), but can it ever reemerge occurs from the black
hole? Hawking maintains no, but Strominger and Vafa have suggested that it
might as radiation.
Evaluation of what has previously been thought to
be a singularity at the center of a black hole is also a subject for string
theory investigation, but so far has been unsuccessful.
Chapter 14
Reflections on Cosmology
Greene reviews standard model of cosmology based
on Big Bang 15 billion years ago, etc. (see Fig. 14.1 p. 356 or this timeline).
At the Planck time
(1.35E-43 sec) after the Big Bang ("ATB"), the
temperature was 1E32 Kelvin. At 1E-5 sec ATB, it had cooled to 1E12
Kelvin and allowed quarks to clump into neutrons and protons. At 1E-2 sec
ATB, primordial nucleosynthesis began. In several thousand years, neutral
atoms formed and the universe became transparent. From then on, photons
have traversed freely. At 1 billion years ATB, galaxies and stars
formed... The cosmic
background radiation is the residual black body radiation cooled by the
expansion of the universe and is now c. 2.7 Kelvin at a current density in space
of c. 4E8 photons/m3. Point particle physics cannot be used to
deal with calculations prior to the Planck time, whereas string theory
can. The time prior to 1E-35 sec ATB (temperatures exceeding 1E28 Kelvin)
is a realm where the 3 nongravity forces were united prior to symmetry
breaking.
However, the "horizon problem" exists:
The observed degree of apparent homogeneity of the cosmic background radiation
is not predicted by the expected spatial proximity and temporal duration
prevailing in the Big Bang. I.e., there would not have been adequate time
for thermal equilibrium to form between regions over the horizon, as it were,
given the finite speed of light. The observed facts can be reconciled via
a period of inflation as proposed by Alan Guth et al 1979 and refined by Linde, Steinhardt, Albrecht, and others. This
solution is compatible with Einstein's general relativity equations and posits a
period during which the universe inflated at an exponentially accelerating
rate. This provides more time in the early stages for communication and
equilibration to occur. Specifically, during the interval 1E-36 ATB
to 1E-34 ATB, the universe would have expanded 1E30 times, and before
that, matter was sufficiently close together to be in equilibrium. [During
the inflationary time, "the energy density of the universe was dominated by a cosmological constant term that later decayed to produce the matter
and radiation that fill the universe today" (quote is from the linked
location).] String theory limits the lower limit of the size of the
universe to the Planck length. Brandenberger and Vafa suggested that at
about the Planck time, three of the previously tightly curled up dimensions are
singled out (or less teleologically, randomly become favorably positioned) for
rapid inflationary expansion to extended spatial dimensions. The number
three is favored by string theory on probability grounds having to do with the
likelihood of particle interactions (which are unlikely if more than
three).
Greene offers additional speculation on alternate
pre-big
bang scenarios and points out that Gabriele
Veneziano has concluded that string theory allows the inflationary sequence
to follow naturally.
M-theory may also allows a less artificially
forced merging of gravity with the three nongravitational forces and avoids the
extreme states of infinite compression and energy. Greene discusses
speculation
about a larger multiverse, in which our universe is simply a local manifestation
or island universe for which an era of inflationary expansion occurred.
Other universes may experience periods of inflation at other "times"
and might have different laws of physics or particle properties, number of
dimensions, etc. But our universe has the properties that have made life
and therefore us as observers possible—the so-called [weak] anthropic
principle. The multiverse may exhibit chaotic variation among the
various universes. Smolin has suggested that every black hole is the seed for a new universe, and that
universes with parameters optimized for forming black holes have a
[reproductive-like] advantage, and come to dominate the population of universes
within the multiverse.
Chapter 15
Prospects [for Unification on the Twenty-First Century]
There are five central unanswered questions of
greatest importance facing string theory:
-
What [if any] is the fundamental principle
underlying string theory (in the same vein that equivalence underlies
general relativity)? Is there a broader principle that underlies
string theory?
-
What are space and time? Is there a raw
precursor to spacetime separate from strings? The problem arises
because we presuppose the existence of space and time in which we place
strings. Is there a fundamental ingredient for spacetime, a
zero-brane?
-
Will string theory lead to a reformulation of
quantum mechanics? Should M-/string theory be quantum mechanical from
the start rather than conceived with classical strings and have quantum
aspects tacked on?
-
Can string theory be tested? (The most
obvious test would be the discovery of superpartner particles.)
-
Are there limits to scientific explanation
beyond which we cannot go?
We are in for even grander surprises in the 21C,
but have been greatly enriched by this quest so far.

